导数极限定理
2021-04-13 16:04:52文/李文源导数极限定理是说:如果f(x)在x0的某领域内连续,在x0的去心邻域内可导,且导函数在x0处的极限存在(等于a),则f(x)在x0处的导数也存在并且等于a。

导数极限定理
首先函数在一点处的导数和在该点处导函数的极限是两个不同的bai概念,前者是直接用导数定义求得,后者是利用求导公式求出导函数的表达式后再求该点处的极限,两者完全可以不相等。
设为数列,A为定数。若对任给的正数ε,总存在正整数N,使得当n>N时,有
|An - A|<ε,
则称数列收敛于A,定数A称为数列的极限,并记作
lim An = A,或 An->A(n->∞),
读作“当n趋于无穷大时,An的极限等于A或An趋于A”。
 有哪些好用的高中数学导数专项教辅书
有哪些好用的高中数学导数专项教辅书导数是函数的综合应用与升华,作为研究函数的重要工具...
2021-04-13 函数的导数怎么求
函数的导数怎么求计算已知函数的导函数可以按照导数的定义运用变化比值...
2021-04-11 如何学好高中数学导数部分
如何学好高中数学导数部分马上就要高考的你,正在经历着被“导数折磨的恐惧吧”...
2021-04-06 x分之一的导数是什么
x分之一的导数是什么x分之一的导数等于-1/x²。导数也叫导函数值。又...
2021-03-22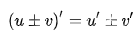 导数运算法则和求导法则
导数运算法则和求导法则不是所有的函数都有导数,一个函数也不一定在所有的点...
2021-03-20 导数的几何意义是什么
导数的几何意义是什么几何意义:函数y=f(x)在x=x0处的导数f′(...
2021-03-20 导数不存在有几种情况
导数不存在有几种情况函数不连续,导数不存在。函数连续,但在该点的左右导...
2021-03-05 x^x的导数
x^x的导数设y=x^x (定义域:x>0),两边取对数得ln...
2021-02-23 logx的导数
logx的导数导数是1/xlna。一般地,函数y=logax(a...
2021-02-22 secx的导数
secx的导数导数:secxtanx。正割是三角函数的正函数(正...
2021-02-09 cotx的导数
cotx的导数cotx导数:-1/sin²x。解过程如下:(co...
2021-02-08 arctan1/x的导数
arctan1/x的导数arctanx的导数是1/(1+x^2)。[arc...
2021-01-15 2x的导数为什么是2
2x的导数为什么是22x的导数是2可以从其几何意义来理解。因为y=2x...
2020-12-10 sin平方x怎么求导
sin平方x怎么求导运算方法有以下两种:1.(sin²x)'=2sin...
2020-12-06 什么是导数
什么是导数导数,也叫导函数值。又名微商,是微积分中的重要基础...
2020-12-03
点击查看 数学知识点 更多内容









