自然对数e的由来
2023-03-11 11:03:06文/苏思楠在1690年,莱布尼茨在信中第一次提到常数e。在论文中第一次提到常数e,是约翰·纳皮尔于1618年出版的对数著作附录中的一张表。但它没有记录这常数,只有由它为底计算出的一张自然对数列表,通常认为是由威廉·奥特雷德制作。第一次把e看为常数的是雅各·伯努利。

自然对数e的来历
e,作为数学常数,是自然对数函数的底数。有时称它为欧拉数,以瑞士数学家欧拉命名;也有个较鲜见的名字纳皮尔常数,以纪念苏格兰数学家约翰·纳皮尔引进对数。它就像圆周率π和虚数单位i,e是数学中最重要的常数之一。
在1690年,莱布尼茨在信中第一次提到常数e。在论文中第一次提到常数e,是约翰·纳皮尔于1618年出版的对数著作附录中的一张表。但它没有记录这常数,只有由它为底计算出的一张自然对数列表,通常认为是由威廉·奥特雷德制作。第一次把e看为常数的是雅各·伯努利。
e在科学技术中用得非常多,一般不使用以10为底数的对数。以e为底数,许多式子都能得到简化,用它是最“自然”的,所以叫“自然对数”。
数学中的e
e (自然常数,也称为欧拉数)是自然对数函数的底数。它是数学中最重要的常数之一,是一个无理数,就是说跟 π 一样是无限不循环小数,在小数点后面无穷无尽,永不重复..
比起我们更熟知的两个无理数圆周率 π 和 √2 不同,它不是由数学家由几何问题上发现而来的,而出自一个金融问题,是用来表示增长率和变化率的常数,很多增长与衰减过程中都出现了 e 的身影。
以e为底的对数函数y=lnx的函数值表称为自然对数表。自然对数表一般由两部分组成,其一是[1,10)的自然对数表,其二是10的各次整数乘幂的自然对数值。对于一个正数x,可以将它表示成十进数的标谁形式:x=q×10n,其中q∈[1, 10),然后分别查表,求出lnq和ln10n,把这两部分相加即得lnx的值。
 自然对数e的由来
自然对数e的由来1742年WilliamJones才发表了幂指数概...
2022-10-11 自然对数的底数
自然对数的底数自然对数的底数是常数e。记作lnN(N>0)。在物...
2019-12-07 正交矩阵定义和性质
正交矩阵定义和性质正交矩阵是指其转置等于逆的矩阵,性质是逆也是正交阵...
2023-03-10 复数的绝对值
复数的绝对值复数没有绝对值的概念,只有模的概念。复数的模:将复...
2023-03-10 什么是复数
什么是复数复数是指把形如z=a+bi(a、b均为实数)的数称...
2023-03-10 y=ln(x+1)的导数
y=ln(x+1)的导数y=ln(x+1)的导数是:y'=1/(x...
2023-03-10 cos的导数
cos的导数cos导数是-sin,反余弦函数(反三角函数之一)...
2023-03-04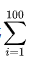 sigma怎么算
sigma怎么算第一个,计算平均值Avg。第二个,计算sigma。...
2023-02-10 e的导数
e的导数因为e是常数,故此,e'=0,即e的导数是...
2023-02-07 0是非负整数吗 为什么
0是非负整数吗 为什么0是非负整数。非负整数是指不是负数的整数集,而零不...
2023-02-04 平行四边形是不是轴对称图形
平行四边形是不是轴对称图形平行四边形不是轴对称图形,但它是中心对称图形,对称...
2023-01-19 直三棱柱的性质
直三棱柱的性质直三棱柱的性质有4点:各个侧面的高相等,底面是三角...
2023-01-14 正三棱柱的性质
正三棱柱的性质正三棱柱是上下底面是全等的两正三角形,侧面是矩形,...
2023-01-14 反函数的二阶导数
反函数的二阶导数反函数的二阶导数:y''=-y&#...
2023-01-14 y=ln(2x+1)的导数
y=ln(2x+1)的导数y=ln(2x+1)的导数是2/(2x+1)。解析...
2023-01-14
点击查看 高中数学知识点 更多内容









