2021年黑龙江高考文科数学试题【word精校版】
2021-06-11 16:35:55文/李傲
绝密★启用前
2021年普通高等学校招生全国统一考试(乙卷)
文科数学
注意事项:
1.答卷前,考生务必将自己的姓名、准考证号填写在答题卡上.
2.回答选择题时,选出每小题答案后,用铅笔把答题卡上对应题目的答案标号涂黑.如需改动,用橡皮擦干净后,再选涂其他答案标号.回答非选择题时,将答案写在答题卡上.写在本试卷上无效.
3.考试结束后,将本试卷和答题卡一并交回.
一、选择题:本题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1.已知全集![]() ,集合
,集合![]() ,则
,则![]() ( )
( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
2.设![]() ,则
,则![]() ( )
( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
3.已知命题![]() ﹔命题
﹔命题![]() ﹐
﹐![]() ,则下列命题中为真命题的是( )
,则下列命题中为真命题的是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
4.函数![]() 的最小正周期和最大值分别是( )
的最小正周期和最大值分别是( )
A.![]() 和
和![]() B.
B.![]() 和2 C.
和2 C.![]() 和
和![]() D.
D.![]() 和2
和2
5.若![]() 满足约束条件
满足约束条件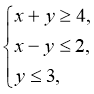 则
则![]() 的最小值为( )
的最小值为( )
A.18 B.10 C.6 D.4
6.![]() ( )
( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
7.在区间![]() 随机取1个数,则取到的数小于
随机取1个数,则取到的数小于![]() 的概率为( )
的概率为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
8.下列函数中最小值为4的是( )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
9.设函数![]() ,则下列函数中为奇函数的是( )
,则下列函数中为奇函数的是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
10.在正方体![]() 中,P为
中,P为![]() 的中点,则直线
的中点,则直线![]() 与
与![]() 所成的角为( )
所成的角为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
11.设B是椭圆![]() 的上顶点,点P在C上,则
的上顶点,点P在C上,则![]() 的最大值为( )
的最大值为( )
A.![]() B.
B.![]() C.
C.![]() D.2
D.2
12.设![]() ,若
,若![]() 为函数
为函数![]() 的极大值点,则( )
的极大值点,则( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
二、填空题:本题共4小题,每小题5分,共20分.
13.已知向量![]() ,若
,若![]() ,则
,则![]() _________.
_________.
14.双曲线![]() 的右焦点到直线
的右焦点到直线![]() 的距离为________.
的距离为________.
15.记![]() 的内角A,B,C的对边分别为a,b,c,面积为
的内角A,B,C的对边分别为a,b,c,面积为![]() ,
,![]() ,
,![]() ,则
,则![]() ________.
________.
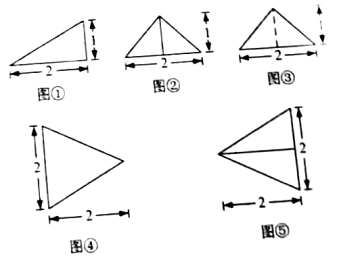
16.以图①为正视图,在图②③④⑤中选两个分别作为侧视图和俯视图,组成某三棱锥的三视图,则所选侧视图和俯视图的编号依次为_________(写出符合要求的一组答案即可).
三、解答题.共70分.解答应写出文字说明,证明过程或演算步骤,第17~21题为必考题,每个试题考生都必须作答.第22、23题为选考题,考生根据要求作答.
(一)必考题:共60分.
17.(12分)
某厂研制了一种生产高精产品的设备,为检验新设备生产产品的某项指标有无提高,用一台旧设备和一台新设备各生产了10件产品,得到各件产品该项指标数据如下:
旧设备 | 9.8 | 10.3 | 10.0 | 10.2 | 9.9 | 9.8 | 10.0 | 10.1 | 10.2 | 9.7 |
新设备 | 10.1 | 10.4 | 10.1 | 10.0 | 10.1 | 10.3 | 10.6 | 10.5 | 10.4 | 10.5 |
旧设备和新设备生产产品的该项指标的样本平均数分别记为![]() 和
和![]() ,样本方差分别记为
,样本方差分别记为![]() 和
和![]() .
.
(1)求![]() ,
,![]() ,
,![]() ,
,![]() ;
;
(2)判断新设备生产产品的该项指标的均值较旧设备是否有显著提高(如果![]() ,则认为新设备生产产品的该项指标的均值较旧设备有显著提高,否则不认为有显著提高).
,则认为新设备生产产品的该项指标的均值较旧设备有显著提高,否则不认为有显著提高).
18.(12分)
如图,四棱锥![]() 的底面是矩形,
的底面是矩形,![]() 底面
底面![]() ,M为
,M为![]() 的中点,且
的中点,且![]() .
.
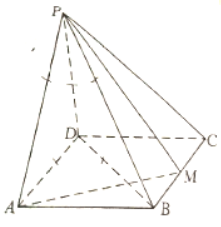
(1)证明:平面![]() 平面
平面![]() ;
;
(2)若![]() ,求四棱锥
,求四棱锥![]() 的体积.
的体积.
19.(12分)
设![]() 是首项为1的等比数列,数列
是首项为1的等比数列,数列![]() 满足
满足![]() .已知
.已知![]() ,
,![]() ,
,![]() 成等差数列.
成等差数列.
(1)求![]() 和
和![]() 的通项公式;
的通项公式;
(2)记![]() 和
和![]() 分别为
分别为![]() 和
和![]() 的前n项和.证明:
的前n项和.证明:![]() .
.
20.(12分)
已知抛物线![]() 的焦点F到准线的距离为2.
的焦点F到准线的距离为2.
(1)求C的方程;
(2)已知O为坐标原点,点P在C上,点Q满足![]() ,求直线
,求直线![]() 斜率的最大值.
斜率的最大值.
21.(12分)
已知函数![]() .
.
(1)讨论![]() 的单调性;
的单调性;
(2)求曲线![]() 过坐标原点的切线与曲线
过坐标原点的切线与曲线![]() 的公共点的坐标.
的公共点的坐标.
(二)选考题:共10分.请考生在第22、23题中任选一题作答.如果多做,则按所做的第一题计分.
22.[选修4-4:坐标系与参数方程](10分)
在直角坐标系![]() 中,
中,![]() 的圆心为
的圆心为![]() ,半径为1.
,半径为1.
(1)写出![]() 的一个参数方程;
的一个参数方程;
(2)过点![]() 作
作![]() 的两条切线.以坐标原点为极点,x轴正半轴为极轴建立极坐标系,求这两条切线的极坐标方程.
的两条切线.以坐标原点为极点,x轴正半轴为极轴建立极坐标系,求这两条切线的极坐标方程.
23.[选修4-5:不等式选讲](10分)
已知函数![]() .
.
(1)当![]() 时,求不等式
时,求不等式![]() 的解集;
的解集;
(2)若![]() ,求a的取值范围.
,求a的取值范围.
 2021年黑龙江高考理综试题【word精校版】2021-06-11
2021年黑龙江高考理综试题【word精校版】2021-06-11 2021年黑龙江高考文综试题【word精校版】2021-06-11
2021年黑龙江高考文综试题【word精校版】2021-06-11 2021年黑龙江高考语文试题【word精校版】2021-06-11
2021年黑龙江高考语文试题【word精校版】2021-06-11 2021年黑龙江高考英语试题【word精校版】2021-06-11
2021年黑龙江高考英语试题【word精校版】2021-06-11 2021年黑龙江高考成绩排名及一分一段表
2021年黑龙江高考成绩排名及一分一段表一分一段表是很重要的填报志愿的依据,也是各大高校划...
2021-06-11 2021黑龙江各大学暑假放假时间安排 什么时候开学
2021黑龙江各大学暑假放假时间安排 什么时候开学2021年黑龙江各大高校的暑假放假时间已经出炉,下...
2021-06-11 2021年黑龙江高考成绩查询时间安排 什么时候出分
2021年黑龙江高考成绩查询时间安排 什么时候出分2021年黑龙江高考成绩预计将于6月24日开通查询...
2021-06-10 2021全国各大高校在黑龙江招生计划
2021全国各大高校在黑龙江招生计划招生计划就是让考生知道自己能不能够报考这个学校,有...
2021-06-10 2021年黑龙江高考语文真题答案解析2021-06-09
2021年黑龙江高考语文真题答案解析2021-06-09 2021年黑龙江高考理综真题答案解析2021-06-09
2021年黑龙江高考理综真题答案解析2021-06-09 2021年黑龙江高考理综真题2021-06-09
2021年黑龙江高考理综真题2021-06-09 2021年黑龙江高考文科数学真题答案解析2021-06-09
2021年黑龙江高考文科数学真题答案解析2021-06-09 2021年黑龙江高考文综真题答案解析2021-06-09
2021年黑龙江高考文综真题答案解析2021-06-09 2021年黑龙江高考语文真题2021-06-09
2021年黑龙江高考语文真题2021-06-09 2021年黑龙江高考文综真题2021-06-08
2021年黑龙江高考文综真题2021-06-08
点击查看 黑龙江高考数学试题 更多内容









